의사의 시작 히포크라테스와 초승달의 히포크라테스

두명의 히포크라테스를 표현한 유튜브 썸네일 - 강태공math

의학의 아버지라고 불리는 히포크라테스(기원전 460-370)는 고대 그리스 페리클레스 시대 의사였습니다.

그의 이름이 들어간 히포크라스 학파는 마술과 철학에서 의학을 분리하여 

의사라는 직업을 만들었으며 고대 그리스 의학을 혁명적으로 발전시켰습니다.

지금 현재 남아있는 기록은 뒤섞여 있어서 그의 생각과 행동이 어떠했는지 자세히는 알려져 있지 않죠.

728x90

페리클레스시대의 의사 히포크라테스

그럼에도 히포크라테스는 고대 의사의 전형으로 기록되어 있고

이전 학파의 생각을 정리하고 시행해 보는 등 환자를 치료하며 수많은 기록을 하였습니다.

치료 의학을 발전시켰으며 히포크라테스 선서도 만들었죠.

12세기의 히포크라테스 선서

수많은 연구 끝에 모든 병은 자연적 원인에 의해 일어난다는 의학적 원리를 세우는 과학적 의학을 창시했습니다.

당시 그리스인들의 사고방식에도 영향을 끼쳐 수많은 의사와 철학자들이 저작한

<히포크라테스 의학 집성>이라는 논문집도 탄생했습니다.

유튜브 영상의 한장면

 

반응형

초승달의 히포크라테스(기원전 470- 410)는 수학사에 중요한 역할을 하였습니다.

원적문제가 고대 그리스의 큰 이슈일 때 사분원 안의 직각삼각형과 원호 사이에 끼어있는 

초승달의 면적 사이의 관계를 알아냈습니다.

자 우리도 히포크라테스의 초승달 문제를 풀어 볼까요?

히포크라테스의 초승달 아래반원을 접으면 바로 알 수 있다.

"직선으로 곡선을 알아낸다"

터무니없는 일만은 아닙니다. 

키오스의 히포크라테스가 이미 곡선으로 둘러싸인 부분의 넓이를 구한 적이 있었습니다.

그것이 바로 히포크라테스의 초승달 이죠.

피타고라스정리를 잘 보여주는 이미지

피타고라스 정리에 따라 직각삼각형의 짧은 변 두 개로 만든 정사각형의 면적은

빗변으로 만들어진 정사각형의 면적과 같습니다.

모양이 변해도 닮음관계가 유지가 되면 넓이가 같음을 보여주는 좋은 이미지

어떻게 변해도 위에 두 개의 면적은 아래 하나의 면적과 같습니다.

반원일 때도 마찬가지이죠.

고대 그리스에서 히포크라테스는 곡선으로 둘러싸인 부분의 넓이를 구했다.

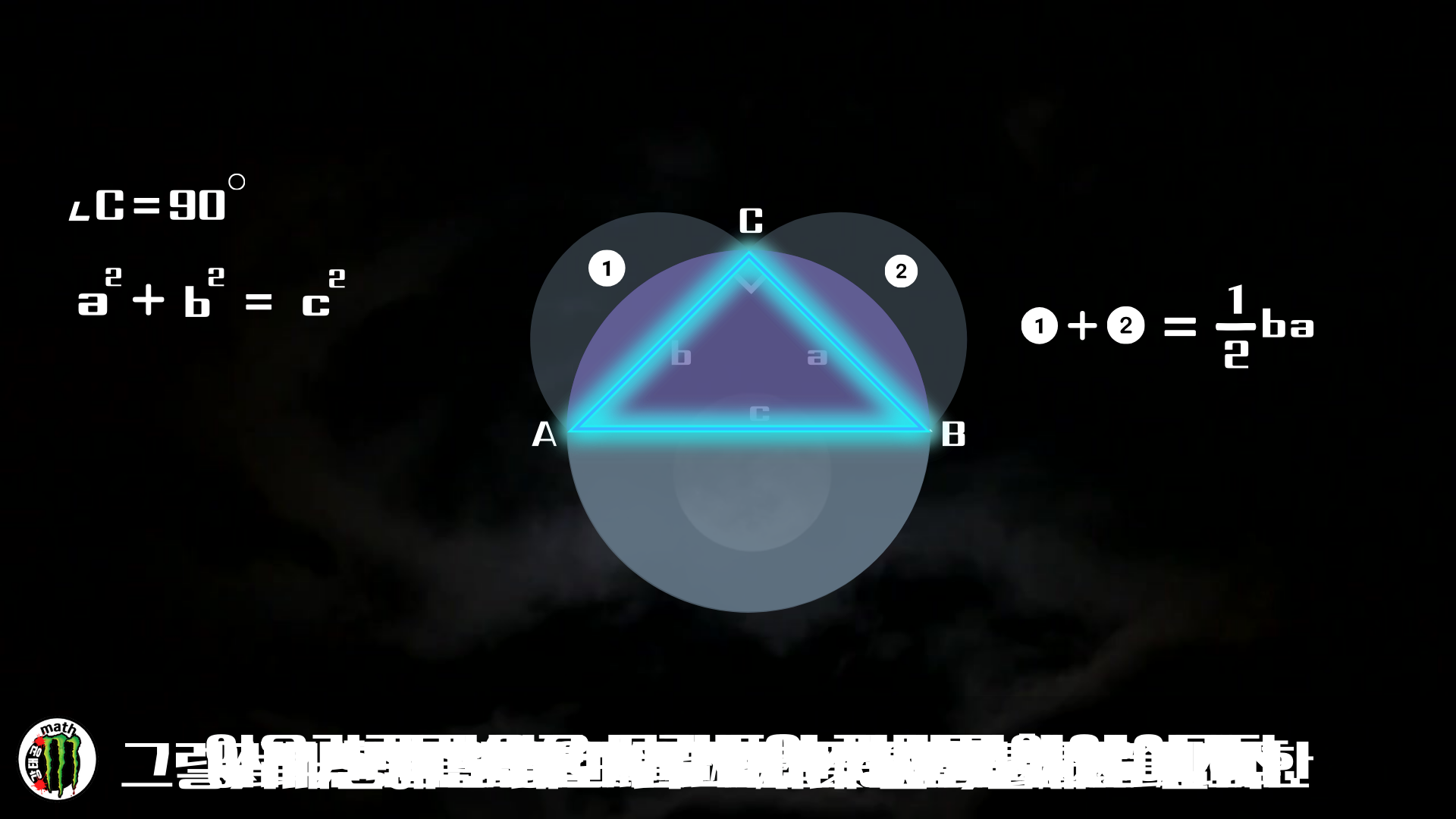
아래 반원을 위로 올리면 공통된 부분을 제외한 곡선으로 둘러싸인 저 부분의 넓이가 

삼각형의 넓이와 같다는 것을 알 수 있습니다.

그렇기 때문에 고대 그리스 시대 원적문제도 할 수 있을 거라고 많은 사람들이 기대를 했었습니다.

쇼츠에서 다루었던 문제도 곡선으로 둘러싸인 부분의 넓이가 

삼각형의 넓이와 같은것을 보여주는 문제입니다.

쇼츠영상에서 보여준 히포크라테스의 초승달문제

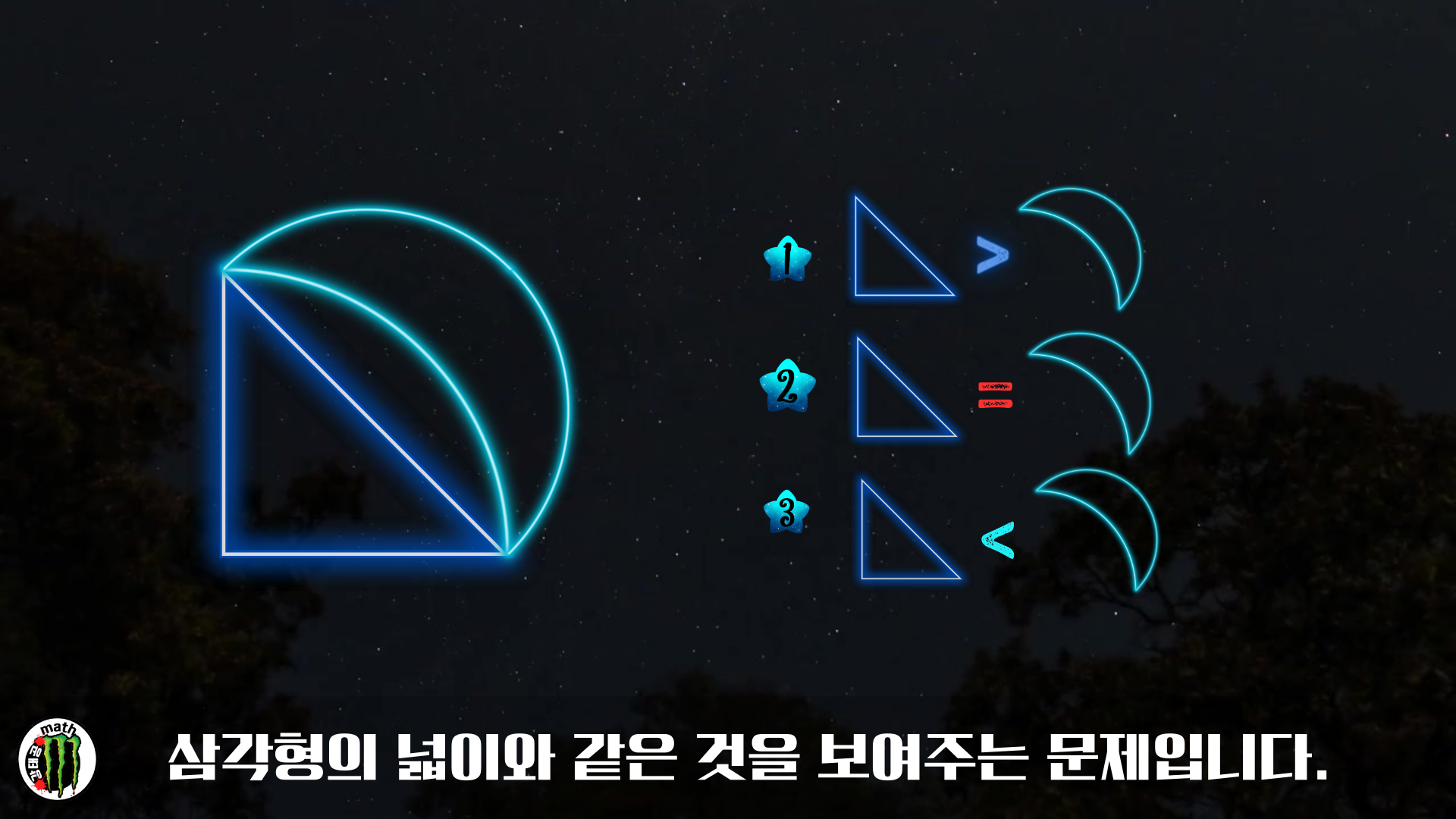
직각이등변삼각형의 짧은 변의 길이를 2라 하면, 4분원의 넓이는 pi임을 알 수 있죠.

그리고 빗변을 지름으로 하는 반원의 넓이도 pi임을 알 수 있습니다.

공통된 부분을 제외하고 보면 삼각형의 넓이와 초승달의 넓이가 같음을 알 수 있다.

두 부분의 넓이가 같으므로 우리는 직각삼각형의 넓이와 초승달모양의 넓이가 같음을 알 수 있는 겁니다.

중학교시절 어렵기만 했던 히포크라테스의 초승달이

접어 올리기만 하면 보이는 것이었다는 사실이 놀라웠습니다.

수학지식채널 강태공수학입니다. 감사합니다. 

유튜브영상 링크입니다.

https://youtu.be/nTMTrG50XDQ?si=ILh-yn74NEp4UnaG