안녕하세요. 강태공수학입니다.

오늘은 세계 여러 나라의 곱셈법과 2초 두 자릿수 곱셈법의 비밀을 보도록 하겠습니다.

현대식 곱셈법과 차이가 있어서 엄청 신선했습니다.
그리고 지금 사용하는 것 보다 새로운 것이 더 좋아 보이는 것은 저만 그런 것일까요?

로마의 곱셈법의 영향이기도 하지만 유럽쪽에는 손가락 곱셈법으로
5보다 큰 수들의 곱셈을 구부린 손가락의 합과 펼쳐진 손가락의 곱으로 표현하기도 합니다.
현재도 사용할 수도 있고 구구단을 외우기 어려울때는 손가락곱셈법이 유용하기도 합니다.


사실 기본적인 것들은 다 외워서 바로 바로 하면 좋겠지만, 모두 다 그럴 수 있는 것은 아니죠.
저도 구구단을 외울때 고생을 많이 했습니다.
자 이제 중국의 곱셈법부터 가볍게 보도록 하죠.

중국의 곱셈법은 자리수를 나누어서 아래와 같이 계산합니다.
현대인이 쓰는 곱셈법과 표기방식만 다르고 같다고 보셔도 될 것 같아요.
물론 표기방식의 가벼운 차이에 의해 속도는 달라질 수도 있겠죠.

저는 학생들을 가르치다보니 너무나도 익숙한 장면이어서, 크게 감흥이 없었답니다.
하지만 안정적이고 자연스럽습니다.

이집트는 중국만큼 깔끔한 영상이 없어서 표현을 못했어요.
그리고 2배법은 고대 이집트에서 곱셈이라는 개념을 만들어내고 실제 사용하게 만들었다는 것이 위대하죠.
문명과 수학을 기획 및 제작을 하면서 사칙연산의 시작과 수의 개념을 만드는 과정이 그 시대의 사람들 입장에서 봤을 때
너무 어려웠답니다. 그런데 2배법은 어려운 곱셈에의 접근을 쉽게 만들어주는 대단함이 있었죠.
고대 이집트의 '아하'와 '2배법'은 정말 뛰어나다고 생각합니다.

다음에 기회될 때 블로그와 유튜브에 올리도록 하겠습니다.
2초 곱셈법이라는 테마에는 맞지 않아 정말 2배씩만 하는 느낌만 보여드리고 넘겼어요.

처음에 보고 많이 놀랐습니다. 와우! 이렇게 좋은 방법이 있을 수 있구나!
눈으로 바로 보인다는 직관성에서 좋은 것 같습니다.
그리고 인도식 곱셈법과 유사성을 5번째 볼 때쯤 알게 되었죠.
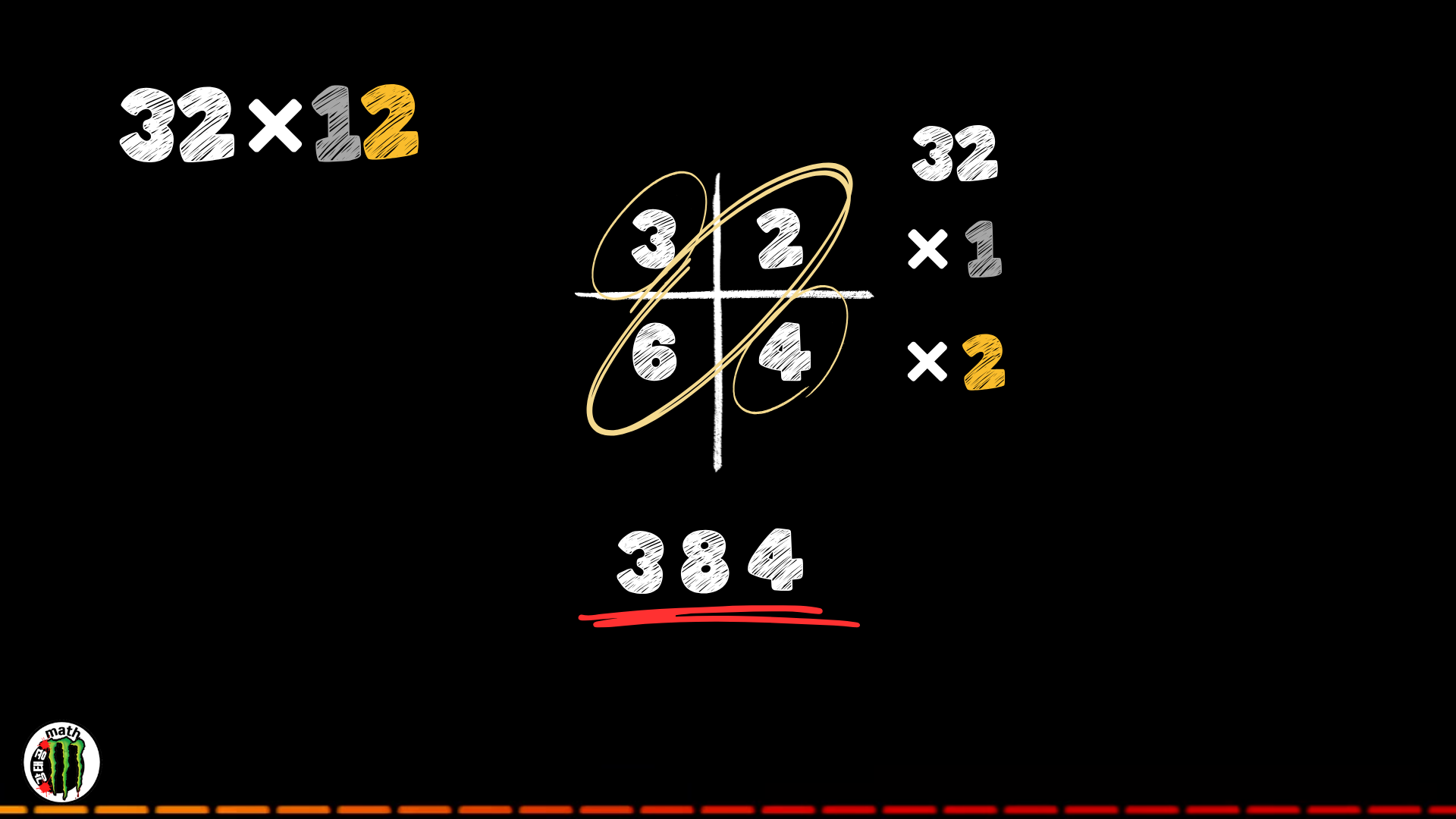
같은 개념을 보는 사람에 따라 또는 보는 나라에 따라 다르게 표현하는구나!
학생들을 가르치다 보면 같은 개념인데도 이해 못 하던 것을 살짝 다르게 표현해 주면 엄청 쉬워합니다.
학생별로 사람별로 자기에 맞는 표현법을 익히는 것이 제일 빠른 것이라 생각해요.
그리고 자기에 맞는 것이 실수를 줄여주죠.

하지만 구구단은 나의 방법이라는 것보다는 암기가 빠른 것은 사실입니다.
그리고 위의 두 가지 특수한 경우는 다른 방법 또는 이해보다는 '더하고', '곱하고'를 익히는 것이 빠르죠.
십의 자리가 1이거나 일의 자리가 1일 때 그 곱셈은 정말 순식간에 할 수 있습니다.

하지만 그렇지 않은 다른 경우들도 모두 2초 만에 할 수는 없죠.(물론 암산천재는 제외)
특수한 경우만 되는 경우니까 알 필요 없지 않습니다.
연산과정에 상당히 나오기 때문에 익혀두면 손해 볼 것은 없죠.
수학을 공부할 때 같은 것을 어떤 시야에서 보는가에 따라 쉬워지기도 어려워지기도 합니다.
추상적인 말이긴 하지만 나에게 맞는 수학의 시야를 가져볼 생각을 하는 것이
앞으로의 수학공부에 많은 도움이 될 것입니다.
수학지식채널 강태공수학이었습니다. 감사합니다.
유튜브영상입니다.
https://youtu.be/AnGZ5usgl9Q
'문명 속에 수학 이야기' 카테고리의 다른 글
| 통합뉴스와의 인터뷰 | 한국 최초 100만 뷰 수학역사영상을 가진 강태공math의 주인공 강태공수학(ktgmath) (252) | 2024.03.05 |
|---|---|
| 기사의 여행 | 오일러의 해밀턴 경로와 Warnsdorff의 휴리스틱 알고리즘 (68) | 2024.02.23 |
| 의사의 시작 히포크라테스와 초승달의 히포크라테스 (92) | 2024.02.16 |
| 수학을 잘하려면 | 문명과 역사속의 수학 '수와 수학의 탄생' | 강태공math 소개 및 기획 의도 (3) | 2024.02.09 |
| 고대 그리스의 수학자 아르키메데스의 원과 원주율 이야기 | 에우독소스의 실진법 (0) | 2024.01.20 |



