무리수와 바빌로니아법, 제단의 수학, 알렉산드리아의 헤론법 그리고 뉴턴랩슨법, 연분수

무리수

강태공math

유리수가 아닌 수를 무리수라고 합니다.

소수로 나타내면 순환하지 않는 무한소수가 됩니다.

실수 가운데 두 정수의 비로 나타나는 수, 즉 분수로 표현할 수 없는 수를 의미합니다.

​

수의 개념은 자연수에서 정수, 정수에서 유리수, 유리수에서 실수로 확장됩니다.

​

​

무리수의 역사

무리수의 시작은 정확하지 않지만, 가장 오래된 기록 중 하나는

기원전 350년 경의 아리스토텔레스의 논증입니다.

Aristotle

 

그의 저서 "분석론 전서(Prior Analytics)"에 나타난 논증은

'피타고라스 정리를 이용하여 대각선의 길이와 한 변의 길이의 비가

 

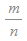
이라고 할 때 모순이 된다.'입니다.

 

만약 m과 n이 둘 다 짝수이면 2로 약분한 다음 생각할 수 있으므로

둘 중 하나는 홀수라고 가정할 수 있습니다.

 

이므로 m은 짝수이고 n은 홀수 이어야 합니다.

 

그러나,​

 

 

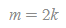
로 놓으면

​

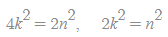
이 되어 n이 짝수이어야 하므로 모순입니다.라고 증명하였습니다.

 

그러나, 피타고라스 학파의 학자들은 한 변의 길이가 1인 정사각형의

대각선의 길이에 해당하는​

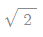
를 하나의 수로 받아들이는 대신 기하적인 양으로만 취급하였다고 합니다.

 

기하학적인 양이란 도형의 길이, 넓이, 부피와 같은 양을 의미합니다.

그 이유는 피타고라스의 가르침이

"모든 수는 두 정수의 비로 나타낼 수 있다."라는 가정을 전제로 하고 있어서

피타고라스의 명예를 지키기 위해서 였다고 전해집니다.

전해지는 이야기 중 이러한 수의 존재를 누설한

히파수스를 바다에 던져버렸다는 이야기가 있습니다.

Heron

기원 후 1세기 경 알렉산드리아의 헤론(Heron)은 삼각형의 세 변의 길이를

이용하여 그 넓이를 계산하는 공식으로 만들었는데,

이를 이용하면 제곱근으로 표현되는 무리수가 등장합니다.

Brahmagupta

 

기원 후 7세기에는 인도의 브라마굽타(Brahmagupta)가 만든 원에 내접하는

사각형의 넓이를 구하는 공식에서도

제곱근 형태의 무리수를 얻을 수 있다고 했습니다.

Euler, L.

1700년대의 수학자 오일러(Euler, L.)는 그의 저서 "대수학 원론"에서

제곱근의 개념과 제곱이 아닌 수의 제곱근의 존재 그리고

이들이 무리수임을 쉽게 이해할 수 있도록 설명하였습니다.

오일러는 제곱뿐만 아니라 세제곱,네제곱 등 거듭제곱의 거듭제곱근 및

이를 좀 더 일반화하여 분수를 지수로 하는 수,

예를 들어

​​

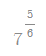
즉,

​

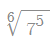
과 같은 무리수에 대해서도 자세하게 설명할 뿐만 아니라

 

이런 무리수들의 더하기, 빼기, 곱하기, 나누기 등에 대해서도

설명하고 있습니다.

Euclid's Elements

 

유클리드는 원론에서 무리수를 "말할 수 없는 길이"라고 불렀습니다.

이것이 라틴어로 "numerus irrationalis"로 번역되어

지금의 "무리수( irrational number )"로 되었습니다.

​

3600여년전의 바빌로니아법부터 인도의 '제단의 수학'

그리고 알렉산드리아의 헤론법 그리고

뉴턴랩슨법 그리고 연분수의 무리수 계산법을

보시고 싶으신 분을 위해 아래 영상을 만들었습니다.

구독과 좋아요는 좋은 품질의 영상을 제작할 힘을 줍니다.

감사합니다.

https://youtu.be/UkwPimg3XXs

​

 

 

#무리수 #근삿값계산법 #바빌로니아법 #연분수 #뉴턴랩슨법 #해론법 #제곱근