곱셈 공식의 활용(합차 공식) | 고대 인도의 제단의 수학

---

인더스강 유역의 뛰어난 문명의 탄생 | 세계적으로 우수한 수학지식

---

인도의 인더스강 유역에는 기원전 3000년부터 기원전 2500년경 고도의 문명이 존재했다고 알려져 있습니다.

실제로 모헨조다로와 하라파에는 계획적으로 건설된 도시가 있었죠.

모헨조다로의 계획적으로 건설된 도시를 보여주는 유튜브의 한장면 ❘ 메소포타미아문명과 비견될정도로 인더스문명도 발전했다.

 그 후 기원전1300년경 북쪽에서 내려온 아리아 민족의 침입으로 원주민이 예속되면서 점차 국가가 형성되었습니다.

 

인도는 적어도 기원전 9세기경까지 아시리아와 바빌로니아와도 교류했다고 전해졌죠.

 

기원전 4세기 말경에는 알렉산드로스 대왕의 인도 침입으로 그리스의 영향도 받았습니다.

 

2세기경 중국에서 불교가 확산된 것에서도 알 수 있듯이, 인도는 중국과도 교류하기 시작했습니다.

여러 거대문명의 영향을 받을 수 밖에 없는 지리적위치

 

이렇듯 원래 뛰어난 문화가 있었던 인도가 주변국의 뛰어난 문화의 영향까지 받아들이게된거죠.

 

당연히 세계적으로 우수한 수학지식을 가질수 밖에 없었던 것입니다.

 

술바수트라스  Śulbasūtras | 원적문제, 무리수, 그리고 정사각형의 작도

---

뛰어난 인도수학에관한 최초의 문헌사료는 기원전6세기경의 <술바수트라스Sulvasutras>가 대표적이죠.

술바수트라스책을 보여드리고 싶었으나...

초기 인도 수학 책이기도 한 ,이 책에서는 제단을 만들기 위한 수학으로

 

'직사각형과 같은 넓이의 정사각형 만들기' (곱셈공식)

'정사각형의 한 변과 대각선의 관계' (무리수)

'넓이가 같은 원과 직사각형'(원적문제) 등

 

기하학적 내용이 증명없이 기술되어 있습니다.

 

증명이 없어서 아쉽기는 하지만 원적문제와 무리수에대해서 기술되어있다는것이 놀라운 사실입니다.

 

주로 입에서입으로 음률과 함께 지식의 전달이 되어왔었기 때문에 최초의 문헌사료는 기원전 6세기이지만

그전부터 이러한 뛰어난 수학지식들을 다루었다는 것을 알 수 있죠.

다만 아쉬운점은 암기와 낭송을 위주로 하다보니 이해하기 쉽게 전달이 되지 않았다는 것입니다.

제단의 모양이 중요했던 베다시대의 제단 원하는것에 맞게 원하는 모양을 만들어야한다.

 

고대인도에서 제사를 지내는 장소나 제단 등의 설치를 할때 직사각형과 같은 넓이의 정사각형이 필요했습니다.

 Unique fire-altar shapes were associated with unique gifts from the Gods.

For instance, "he who desires heaven is to construct a fire-altar in the form of a falcon";

"a fire-altar in the form of a tortoise is to be constructed by one desiring to win the world of Brahman"

and "those who wish to destroy existing and future enemies should construct a fire-altar in the form of a rhombus"

종교적인 측면이 강하기때문에 해석의 논란의 여지가 있어 영문으로 올려드립니다. (Unique shapes / unique gifts ) 

원하는 것에 맞게 원하는 모양을 만들어야 한다는 것이죠. 이렇게 제단의 모양을 중시여겼던 베다시대였습니다. 

하늘을 원한다면 매의 모양으로

 

---

합차공식이라고도 불리는 곱셈공식의 활용이 2600년전에도 사용되었던 것이죠.

 

자 그럼 고대인도의 직사각형과 같은 넓이의 정사각형의 작도를 보도록하죠.

 

하나의 직사각형ABCD가 있습니다.

긴변에서 짧은변의 길이를 제외한 남은선분의 중점을 찍어

긴변을 두개의 선분으로 나누어줍니다.

그림에서는 AG와 GD가 되겠죠.

 AG의 길이를 a, GD의 길이를 b라고하면 직사각형의 넓이는 

(b+a)(b-a)가되죠. b^2-a^2이 됩니다.

이렇게 색깔과 움직임을 넣어서 설명하면 이해가 쉽다.

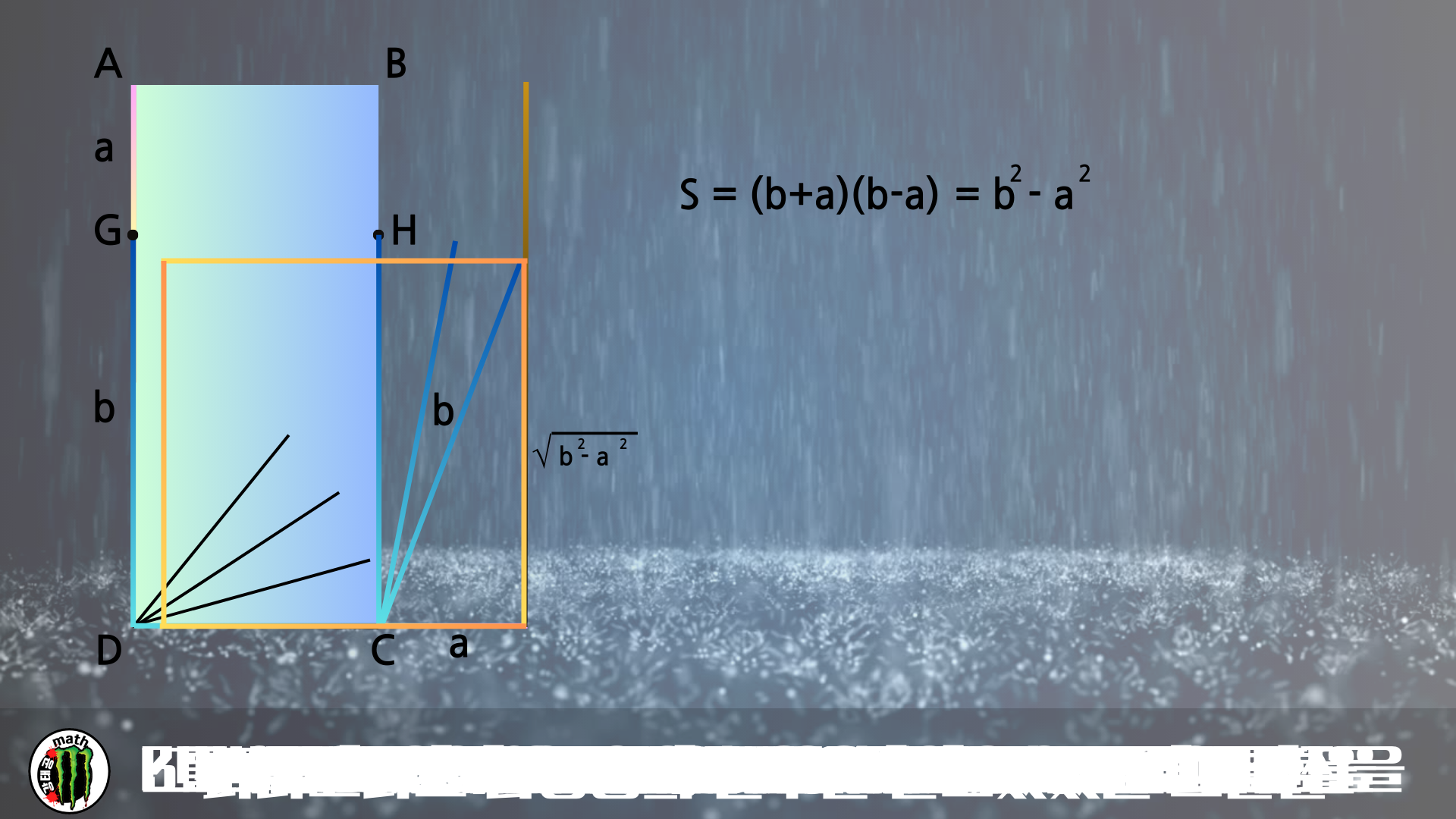
피타고라스정리에 의해 b를 빗변으로하고 a를 밑변으로하는 직각삼각형을 만들면 

우리는 직사각형과 같은 넓이의 정사각형의 한변을 만들 수 있는거죠.

 

그리고 이렇게 정사각형을 그려주면 되는겁니다. 참 쉽죠~

 

음률과 함께구전되었던 고대 인도의 수학에서의 곱셈공식의 활용이었습니다. 감사합니다.

 

https://youtu.be/3q_aa3A3WPc?feature=shared