hello. This is Kang Tae Gong Mathematics.

Today we will look at the secrets of multiplication methods in various countries around the world
and the 2-second double-digit multiplication method.

It was very refreshing because it was different from the modern multiplication method.
And is it just me who seems to like the new one better than the one I'm using now?

This may be due to the influence of the Roman multiplication method,
but in Europe it is also known as the finger multiplication method.
Multiplication of numbers greater than 5 is also expressed as the sum of the bent fingers multiplied by the spread fingers.
You can still use it now, and the finger multiplication method is useful
when it is difficult to memorize the multiplication table.


In fact, it would be good to memorize all the basic things and do them right away, but that is not possible for everything.
I also had a hard time memorizing the multiplication table.
Now, let’s take a quick look at the Chinese multiplication method.

The Chinese multiplication method divides the digits and calculates as follows.
I think you can think of it as the same,
with only the multiplication method and notation used by modern people being different.
Of course, the speed may vary due to slight differences in notation methods.

It was a very familiar scene to me as I taught students, so I wasn't very impressed.
But it is stable and natural.

I couldn't express Egypt because it doesn't have as clean a video as China.
And the great thing about the doubling method is that it created the concept of multiplication in ancient Egypt
and put it into practical use.
From the perspective of the people of that era, the process of starting the four basic arithmetic operations
and creating the concept of numbers while planning and producing Civilization and Mathematics was very difficult.
However, the doubling method had the great advantage of making difficult multiplication easier.
I think the 'aha' and 'double method' of ancient Egypt are truly outstanding.

I will post it on my blog and YouTube next time I have the chance.
It doesn't fit the theme of the 2-second multiplication method, so I just showed the feeling of doubling and passed on.
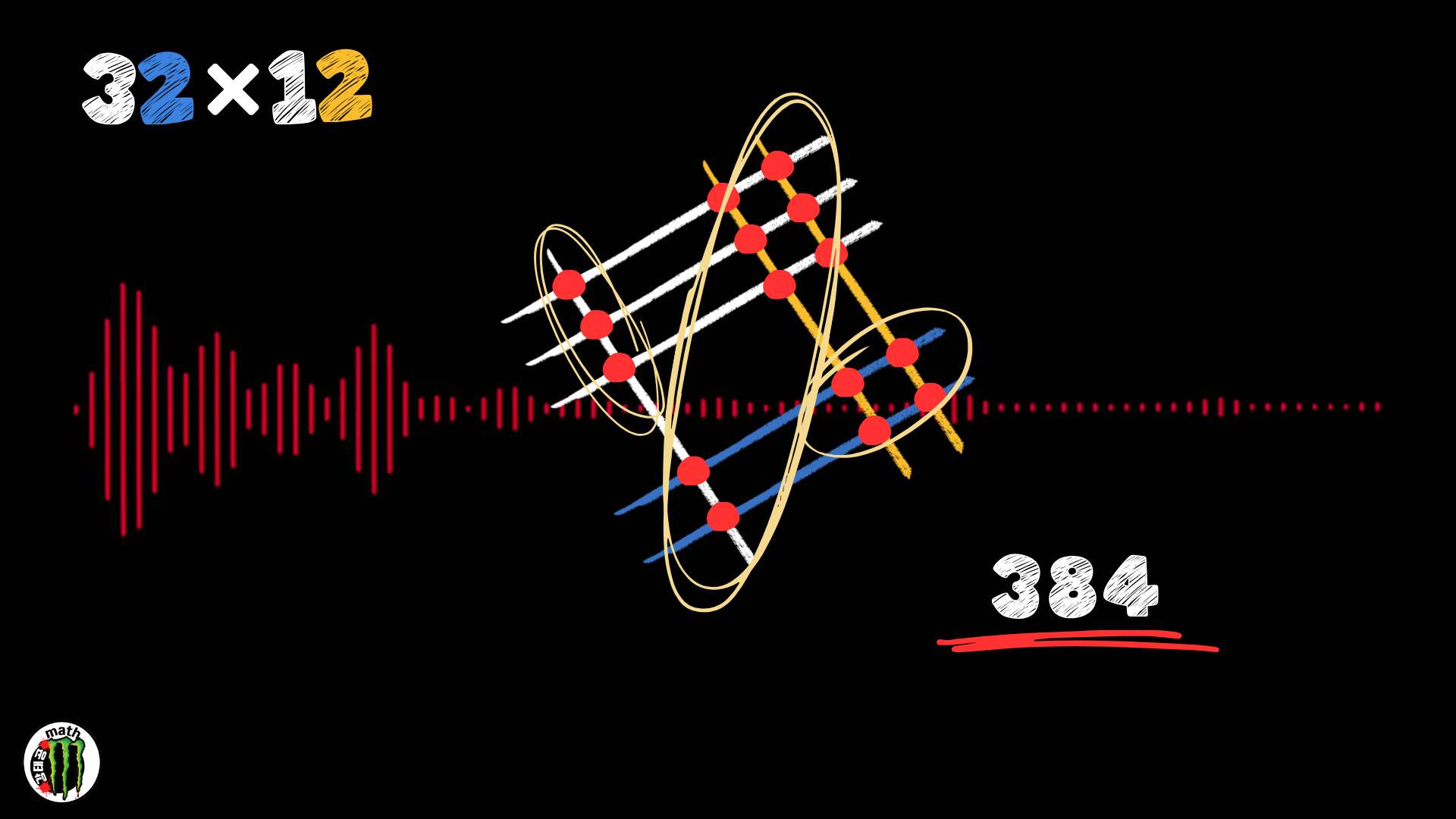
I was very surprised when I first saw it. wow! There can be such a good way!
I think it's good because it's intuitive because you can see it right away.
And I realized the similarity with the Indian multiplication method by the 5th time I saw it.

The same concept is expressed differently depending on the viewer or the country from which it is viewed!
When teaching students, it becomes much easier if you express the same concept in a slightly different way.
I think the fastest way is for each student to learn a method of expression that suits them.
And what suits you reduces mistakes.

However, it is true that memorization of the multiplication table is faster than that it is my method.
And for the above two special cases, it is faster to learn 'add' and 'multiply' than other methods or understanding.
When the tens place is 1 or the ones place is 1, the multiplication can be done really quickly.

But in other cases, you can't do it all in 2 seconds (except for mental arithmetic genius, of course).
Even if it is only a special case, you need to be aware of it.
Since it comes up a lot in the calculation process, there is nothing to lose if you learn it.
When studying math, it can become easier or more difficult depending on what perspective you look at the same thing.
Although it is an abstract statement,
thinking about having a perspective on mathematics that suits you will be very helpful in your future mathematics studies.
It was ktgmath, a math knowledge channel. thank you
This is a YouTube video.https://youtu.be/AnGZ5usgl9Q



